El conocimiento del cálculo de giros y desplazamiento es necesario para poder entender los efectos que producen las cargas externas en el interior de la viga.
El presente trabajo esta basado en uno de los métodos para calcular el giro y desplazamientos en cualquier punto de una viga sometida a cargas utilizando el diagrama de momentos.
Contiene cinco problemas resueltos según el marco teórico que ayudará al lector a tener base para la comprensión de temas posteriores y un glosario de palabras técnicas de uso seguido que facilitará la interpretación en el desarrollo del trabajo.
I. GENERALIDADES
1.1 Objetivos:
El objetivo principal es aplicar los conocimientos previos de diagramación, en este caso del momento flector, para calcular pendientes y deflexiones en una viga sometida a cargas puntuales o distribuidas.
a) Teorema 1:
· Entender la relación de la curvatura con la pendiente de la elástica.
· Establecer las condiciones iniciales, de giros, y utilizar medios diferenciales para el cálculo de la pendiente.
b) teorema 2:
· Establecer una relación entre la curva y la deflexión.
· Calcular el desplazamiento vertical de la elástica usando el diagrama de momentos.
1.2 Glosario
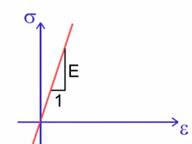
a) Módulo de elasticidad: (E)
El módulo de elasticidad o módulo de Young es un parámetro que caracteriza el comportamiento de un material elástico, según la dirección en la que se aplica una fuerza. Siendo una constante independiente del esfuerzo y es siempre mayor que cero.
b) Eje neutro:
Es la intersección de la superficie neutra (superficie que no sufre deformación e=0) con la sección transversal.
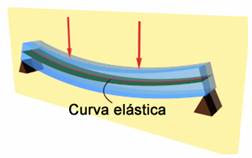
c) Curva elástica:
Llamada también Elástica. La ecuación de la elástica es la ecuación diferencial que, para una viga de eje recto, permite encontrar la forma concreta de la curva elástica. Concretamente la ecuación de la elástica es una ecuación para el campo de desplazamientos que sufre el eje de la viga desde su forma recta original a la forma curvada o flectada final.
d) Giro (θ):
Al trazar rectas tangentes a la curva elástica estas forman con la horizontal ángulos muy pequeños, estos ángulos son los ángulos de giro de la curva elástica.
II. MARCO TEÓRICO
Método De Área Momento
Este método se basa en la relación que existe entre el momento M y la curvatura y proporciona medios prácticos y eficientes para calcular la pendiente y la deflexión de la curva elástica de vigas y pórticos.
El método tiene dos teoremas. El primero relaciona la curvatura con la pendiente de la curva elástica y el segundo la curvatura con la deflexión.
Método De Área Momento
Este método se basa en la relación que existe entre el momento M y la curvatura y proporciona medios prácticos y eficientes para calcular la pendiente y la deflexión de la curva elástica de vigas y pórticos.
El método tiene dos teoremas. El primero relaciona la curvatura con la pendiente de la curva elástica y el segundo la curvatura con la deflexión.
2.2 Teorema 2:
Por teoría de los ángulos pequeños tenemos:
 , si sumamos todos los desplazamientos verticales obtenemos la desviación vertical entre las tangentes en A y B.
, si sumamos todos los desplazamientos verticales obtenemos la desviación vertical entre las tangentes en A y B.
El teorema es: “La desviación de la tangente en un punto A sobre la curva elástica con respecto a la tangente prolongada desde otro punto B, es igual al momento del área bajo la curva
 entre los puntos Ay B con respecto a un eje A.
entre los puntos Ay B con respecto a un eje A.Se cumple siempre cuando en la curva no haya discontinuidades por articulaciones.
Esta desviación siempre es perpendicular a la posición original de la viga y se denomina flecha.
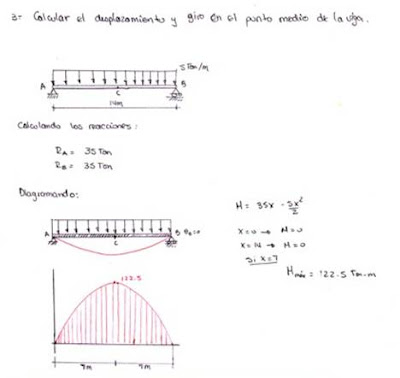
III. EJERCICIOS
5.- calcular la desviación total de la viga:
IV. ANEXOS:
El techo proporciona una carga distribuida a la viga, siendo ésta menor en los extremos y mayor en el centro de la viga, a esto se suma el peso propio del techo. La acción del viento sobre el techo también presenta un tipo de carga distribuida sobre la viga.
La viga transmite la carga a la columna, en los apoyos de esta la deflexión es nula.






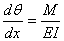

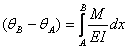



















6 comentarios:
no se ven la mayoria de los numeros de los problemas resueltos
podriais colgarlos con los numeros mas grandes y claros ? gracias
hola, puedes expllicar bien con que criterio eliminas algunos giros en los problemas?
POR LO VISTO EL QUE HIZO ESOS EJERCICIOS NO TIENE EL CRITERIO ADECUADO DE PENDIENTES ..!SOBRE TODO ME LLAMO LA ATENCION EL EJERCICIO 3 ..! NO SABIA QUE HABIA GIRO EN EL MEDIO DE LA VIGA.!! MUY MAL.!! (N)
Muy buena
Publicar un comentario